Whether you are a professional or amateur scientist, engineer or mathematician, if you need to make numerical calculations and plots quickly and easily, then PDL (Perl Data Language) is certainly one of the best free software tools to use. PDL has everything that similar high-level, proprietary, numerical calculation languages (like IDL or MATLAB) have. And it certainly comes with all the features you would expect to have in a numerical calculation package.
Introduction
In this article, I will explore a fun application of the numerical calculation field: the Mandelbrot fractal. To generate fractals you need to perform several computations and then plot the results. The examples that follow are also simple enough for anyone to follow, but have enough features to get a feel for the language used. For this particular task, high-level, numerical calculation languages are the ideal tool. They provide a rapid development cycle due to its high-level nature. It is also easy to generate quality plots with these tools. And, as you shall see later, the speed performance penalty you pay by using these languages is relatively minor.
The Mandelbrot fractal example reviewed in this article will be developed in both proprietary and free software languages: PDL, IDL, MATLAB and Octave. This will allow us to compare them qualitatively in a table highlighting the pros and cons of each language. Also, a quantitative benchmark comparison will be done to illustrate the speed of each one of the languages. For comparison purposes, C and FORTRAN code for these examples will also be shown.
The Mandelbrot fractal
The Mandelbrot set is one of the most popular fractals
According to Wikipedia, a fractal is a rough or fragmented geometric shape that can be subdivided into parts, each of which is (at least approximately) a reduced size copy of the whole. The Mandelbrot set is one of the most popular fractals. In this article I will color the fractals in a slightly different and artistic way (as seen in figure 1). The Mandelbrot fractal is generated by iterating a mathematical relationship between complex numbers (see Complex Number Arithmetic for a quick introduction to complex numbers). Starting with a zero value of a complex variable (z), the fractal is materialised by iterating the following assigment:
z = z * z + k,
...where k is a complex number which is kept constant throughout the iterations. The final value of z depends very much on the value of the complex number k. For some values of k, the final z converges to a certain finite value and for some others, z diverges to infinity. To avoid numerical problems with the divergences in the calculations we will introduce a programming trick that consists of constraining the z values between -5 and 5 after each iteration. In the final fractal image, the x axis will represent the real values of k and the y axis its imaginary values. In the Mandelbrot fractal, normally the divergent z values are given one color and the convergent ones another. The frontier between one color and the other is a fractal. Here I will color the images using a rainbow palette to plot the values of the formula:
image = log (sqrt(Re(z) * Re(z) + Im(z) * Im(z)) + 1)
...where Re and Im denote the real and imaginary part of z respectively. The final Madelbrot fractal image can be seen in figure 1.

PDL
PDL is an extension of the Perl language for number crunching and scientific plotting
PDL is an extension of the Perl language for number crunching and scientific plotting. Because of its Perl heritage it has the clean syntax of a well settled programming language. You can also use one of the wealth of available module-packages in the Perl archive (CPAN), to use the language for other purposes like database access, date handling, inter-process communication, GUI toolkit, just to name a few.
Installing PDL
Unfortunately, PDL is not installed by default on many of the popular GNU/Linux distributions. Even worse, some distributions have the PDL related packages missing or partly broken. If you are running a GNU/Linux distribution based on Debian (Ubuntu, Knoppix, etc.), and have access to the regular Debian repositories, it is fairly easy to install PDL. You should install the pdl, pgplot5 and pgperl packages in order to follow the examples in this article. This can be done (as root) via the usual:
apt-get install pdl pgplot5 pgperl
If this is not your case, follow the instructions in Installing PDL the quick and easy way.
The PDL command line
Once you have PDL installed you should be able to run it in the command line. For this just type perldl on a terminal.
It should greet you with a message like:
xcalbet@debian:~$ perldl
perlDL shell v1.33
PDL comes with ABSOLUTELY NO WARRANTY. For details, see the file 'COPYING' in the PDL distribution. This
is free software and you are welcome to redistribute
it under certain conditions, see the same file for
details.
ReadLines, NiceSlice, MultiLines enabled
Reading PDL/default.perldlrc...
Found docs database /usr/local/lib/perl/5.8.4/PDL/pdldoc.db
Type 'help' for online help
Type 'demo' for online demos
Loaded PDL v2.4.2
perldl>
You can try out now some of PDL features by typing demo after the PDL prompt:
perldl> demo
This will provide you with a list of demos you can try. You should also check that the plotting library you will be using inside PDL is working properly. To do this type:
perldl> demo pgplot
Some nice graphs should appear on your screen. If this is not the case have a look in Installing PDL the quick and easy way.
In the next section, I will explain how to generate the Mandelbrot fractal step-by-step using the PDL command line, so you can learn the basics of PDL.
The Mandelbrot fractal with PDL
Perl scalars are usually denoted by a variable name preceded by a dollar sign. These variables can contain only one object which can be a string, a more complex object, or, as is in this particular case, a numerical value,
perldl> $npts=200;
perldl> $niter=10;
Here the number of points along the side of the square fractal image and the number of iterations for the Mandelbrot calculation are stored in their respective variables. We can have a look at the contents of these variables with the print function:
perldl> print $npts;
200
The basic building blocks of the PDL language are n-dimensional arrays usually referred to as “piddles”. A piddle is stored in a scalar Perl variable, like the real and imaginary part of z, $zRe and $zIm:
perldl> $zRe=zeroes(double,$npts,$npts);
perldl> $zIm=zeroes(double,$npts,$npts);
In this case, two-dimensional, double-precision, square arrays of zeroes are generated with the zeroes function. Its size is given by the $npts variable.
You can now generate the matrices that will represent the k constant by using the xlinvals and ylinvals functions. These functions assign different values for each column or row respectively within a certain range.
perldl> $kRe=$zRe->xlinvals(-1.5,0.5);
perldl> $kIm=$zIm->ylinvals(-1,1);
We can subset the $kRe and $kIm matrices with the slice method to have a better feeling of what the xlinvals and ylinvals functions do:
perldl> print $kRe->slice('0:4,0:4');
[
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
[ -1.5 -1.497998 -1.495996 -1.493994 -1.491992]
]
perldl> print $kIm->slice('0:4,0:4');
[
[ -1 -1 -1 -1 -1]
[ -0.997998 -0.997998 -0.997998 -0.997998 -0.997998]
[ -0.995996 -0.995996 -0.995996 -0.995996 -0.995996]
[-0.99399399 -0.99399399 -0.99399399 -0.99399399 -0.99399399]
[-0.99199199 -0.99199199 -0.99199199 -0.99199199 -0.99199199]
]
You can now start a loop to make $niter iterations on the numerical calculations. The syntax of loops in Perl is very similar to the C language one:
perldl> for($j=0;$j<$niter;$j++){
The PDL prompt will change to:
..{ >
The meaning of which is that it is expecting you to introduce at some point the end of the loop.
Mathematical operations between piddles are usually performed on an element per element basis. This happens when both piddles have exactly the same dimensions. So, if you multiply or add several piddles of the same size, these operations will be performed element per element and the end result will be assigned to a matrix the same size as the original ones. You can use this property to make the iterations required for the Mandelbrot set (z = z * z + k), which, when split into real and imaginary parts, looks like(see Complex Number Arithmetic):
..{ > $qRe=$zRe*$zRe-$zIm*$zIm+$kRe;
..{ > $qIm=2*$zRe*$zIm+$kIm;
You should next apply the trick of constraining the values between -5 and 5 after each iteration, this is done in PDL using the clip function:
..{ > $zRe=$qRe->clip(-5,5);
..{ > $zIm=$qIm->clip(-5,5);
And now introduce the end of the loop:
..{ > }
The calculations will take a few seconds on a relatively modern PC. When the computations are finished the PDL prompt will appear again.
Perl is a modular language with the possibility of loading other modules if needed. To plot the fractal you’ll need to load two modules with the use statement:
perldl> use PDL::Graphics::PGPLOT::Window;
perldl> use PDL::Graphics::LUT;
You can now open a window for plotting:
perldl> $w=PDL::Graphics::PGPLOT::Window->new(Device=>'/xserve');
If everything works perfectly, an empty window should show up on your screen. You can now select a color palette and calculate the final image:
perldl> $w->ctab( lut_data('rainbow2') );
perldl> $image=log( sqrt($zRe**2+$zIm**2) + 1);
Now you are finally ready to plot the Mandelbrot fractal:
perldl> $w->imag($image);
An image similar to the one in figure 1 should show up. As you have seen, making numerical calculations in PDL is easy and straightforward. Making plots of your data is also a breeze.
All these PDL statements, which you have just seen, can be compiled in a Perl program called mandel.pl, which appears in the listing below.
#!/usr/bin/env perl
# PDL code to generate a Mandelbrot fractal
use PDL;
use PDL::Graphics::PGPLOT::Window;
use PDL::Graphics::LUT;
# Number of points in side of image and
# number of iterations in the Mandelbrot
# fractal calculation
$npts=1000;
$niter=51;
# Generating z = 0 (real and
# imaginary part)
$zRe=zeroes(double,$npts,$npts);
$zIm=zeroes(double,$npts,$npts);
# Generating the constant k (real and
# imaginary part)
$kRe=$zRe->xlinvals(-1.5,0.5);
$kIm=$zIm->ylinvals(-1,1);
# Iterating
print "Calculating Mandel\n";
for($j=0;$j<$niter;$j++){
# Calculating q = z*z + k in complex space
# q is a temporary variable to store the result
$qRe=$zRe*$zRe-$zIm*$zIm+$kRe;
$qIm=2*$zRe*$zIm+$kIm;
# Assigning the q values to z constraining between
# -5 and 5 to avoid numerical divergences
$zRe=$qRe->clip(-5,5);
$zIm=$qIm->clip(-5,5);
}
# Lines below this one are commented out when making
# the benchmark.
# Generating plot
print "Generating plot\n";
# Opening a window for plotting
$w=PDL::Graphics::PGPLOT::Window->new(Device=>'/xserve');
# Changing the color palette
$w->ctab( lut_data('rainbow2') );
# Generating the image to plot
$image=log( sqrt($zRe**2+$zIm**2) + 1);
# Plotting the image
$w->imag($image);
Zooming into the Mandelbrot fractal
It is now very easy to zoom into the Mandelbrot fractal by “zooming” into the initial k values. You can achieve this by changing the initial k assignment to:
# Generating the constant k
$kRe=$zRe->xlinvals(0.34,0.44);
$kIm=$zIm->ylinvals(0.29,0.39);
The result is shown in figure 2.

More on PDL
There is more to PDL than what you have just seen here. One of the features that makes it powerful and sets it apart from other languages, is the behaviour of the mathematical operators when the matrices involved do not have the same dimensions. These properties are fairly well described in the PDL indexing manual page and will not be discussed in detail here.
Another important feature is the many functions it has for manipulating array sizes and contents. We have seen some of them like zeroes and xlinvals, but there are many others that make array programming life much easier than with other equivalent languages.
There are some excellent introductions to PDL. Some of them are listed in the bibliography.
But it’s time now to look at the competition.
IDL
IDL is a proprietary and certainly not free number-crunching-oriented language very similar to PDL
IDL is a proprietary and certainly not free number-crunching-oriented language very similar to PDL. The mathematical operators are mainly used on an element per element basis like PDL. Although, naturally, other types of operations exist, like matrix multiplication. The IDL version of the Mandelbrot program is shown in the listing below. The comments in the code listing give an explanation of its contents.
pro mandel
; IDL code to generate a Mandelbrot fractal
; Number of points in side of image and
; number of iterations in the Mandelbrot
; fractal calculation
npts=1000
niter=51
; Generating z = 0 (real and
; imaginary part)
zRe=dblarr(npts,npts)
zIm=dblarr(npts,npts)
; Generating the constant k (real and
; imaginary part)
a=dindgen(npts,npts)
kRe=a mod npts
kIm=float(floor(a/npts))
kRe=kRe*2.0/(npts-1.)-1.5
kIm=kIm*2.0/(npts-1.)-1
; Iterating
print,"Calculating Mandel"
for j=1,niter do begin
; Calculating q = z*z + k in complex space
; q is a temporary variable to store the result
qRe=zRe*zRe-zIm*zIm+kRe
qIm=2*zRe*zIm+kIm
; Assigning the q values to z constraining between
; -5 and 5 to avoid numerical divergences
zRe = qRe < 5
zRe = zRe > (-5.)
zIm = qIm < 5
zIm = zIm > (-5.)
end
; Lines below this one are commented out when making
; the benchmark.
; Generating plot
print,"Generating plot"
; Opening a window for plotting
device,decomposed=0,retain=2
Window,0,Xsize=400,Ysize=400
; Generating the image to plot
image=alog( sqrt(Re^2+Im^2) + 1)
; Plotting the image
tvscl,image
end
MATLAB
MATLAB is a proprietary language mainly targeted at mathematical calculations
MATLAB is a proprietary language mainly targeted at mathematical calculations. It is well suited for two dimensional matrices but can also work efficiently with higher dimensional matrices. It is also, as will be shown in the benchmarks, a relatively slow executing language. One of its advantages being that it has a huge number of easy to use mathematical functions available, from ordinary differential equation solving, to minimisation problems, etc. In the following listing you can see the Mandelbrot program in MATLAB with comments explaining the code.
% MATLAB and Octave code to generate a Mandelbrot fractal
% Number of points in side of image and
% number of iterations in the Mandelbrot
% fractal calculation
npts=1000;
niter=51;
% Generating z = 0 (real and
% imaginary part)
zRe=zeros(npts,npts);
zIm=zeros(npts,npts);
% Generating the constant k (real and
% imaginary part)
kRe=repmat(linspace(-1.5,0.5,npts),npts,1);
kIm=repmat(linspace(-1,1,npts)',1,npts);
% Iterating
for j=1:niter
% Calculating q = z*z + k in complex space
% q is a temporary variable to store the result
qRe=zRe.*zRe-zIm.*zIm+kRe;
qIm=2.*zRe.*zIm+kIm;
% Assigning the q values to z constraining between
% -5 and 5 to avoid numerical divergences
zRe=qRe;
qgtfive= find(qRe > 5.);
zRe(qgtfive)=5.;
qltmfive=find(qRe<-5.);
zRe(qltmfive)=-5.;
zIm=qIm;
hgtfive=find(qIm>5.);
zIm(hgtfive)=5.;
hltmfive=find(qIm<-5.);
zIm(hltmfive)=-5.;
end
% Lines below this one are commented out when making
% the benchmark.
% Generating plot
% Generating the image to plot
ima=log( sqrt(zRe.*zRe+zIm.*zIm) + 1);
% Plotting the image
imagesc(ima);
exit
Octave
Octave is a free software clone of MATLAB
Octave is a free software clone of MATLAB. In fact, its main advantage is that it’s an almost perfect clone of MATLAB. Some code written for MATLAB will most probably run with very few hitches, if any, in Octave. In fact, the Octave Mandelbrot example is exactly the same as the MATLAB one, shown in the previous MATLAB listing. Being such a perfect MATLAB clone it shares all of MATLAB’s advantages and all its disadvantages like its speed. The only exception being its price.
C and FORTRAN77
C and FORTRAN77 are low-level languages, which do not compare well in developing time with the other numerical calculation and plotting languages, but are certainly very fast in execution time. They have been included here for the benchmark comparison just to give an idea of how much slower the high-level languages are by comparison to these low-level, more traditional languages. The following listing shows the Mandelbrot program in C.
#include <stdio.h>
#include <math.h>
// Number of points in side of image
#define NPTS 1000
int main(void) {
double zRe[NPTS][NPTS];
double zIm[NPTS][NPTS];
double kRe[NPTS][NPTS];
double kIm[NPTS][NPTS];
double qRe[NPTS][NPTS];
double qIm[NPTS][NPTS];
long int i,j,k,niter;
// Number of iterations in the Mandelbrot
// fractal calculation
niter=51;
for (i=0;i<NPTS;i++) {
for (j=0;j<NPTS;j++) {
// Generating z = 0 (real and
// imaginary part)
zRe[i][j]=0.;
zIm[i][j]=0.;
// Generating the constant k (real and
// imaginary part)
kRe[i][j]=(double)i*2.0/((double)NPTS-1.)-1.5;
kIm[i][j]=(double)j*2.0/((double)NPTS-1.)-1.;
}
}
// Iterating
//printf("Calculating Mandel\n");
for(k=0;k<niter;k++){
for (i=0;i<NPTS;i++) {
for (j=0;j<NPTS;j++) {
// Calculating q = z*z + k in complex space
// q is a temporary variable to store the result
qRe[i][j]=zRe[i][j]*zRe[i][j]-zIm[i][j]*zIm[i][j]+kRe[i][j];
qIm[i][j]=2.*zRe[i][j]*zIm[i][j]+kIm[i][j];
// Assigning the q values to z constraining between
// -5 and 5 to avoid numerical divergences
zRe[i][j]=qRe[i][j];
zIm[i][j]=qIm[i][j];
if (zRe[i][j] < -5.) zRe[i][j]=-5.;
if (zRe[i][j] > 5.) zRe[i][j]=5.;
if (zIm[i][j] < -5.) zIm[i][j]=-5.;
if (zIm[i][j] > 5.) zIm[i][j]=5.;
}
}
}
// Lines below this one are commented out when making
// the benchmark.
// Writing image to STDOUT
for (i=0;i<NPTS;i++) {
for (j=0;j<NPTS;j++) {
printf("%f ",log( sqrt(zRe[i][j]*zRe[i][j]+zIm[i][j]*zIm[i][j]) + 1.));
}
printf("\n");
}
}
The listing in FORTRAN is shown below.
program mandel
! FORTRAN77 code to generate a Mandelbrot fractal
implicit none
integer npts
! Number of points in side of image
parameter (npts=1000)
real*8 zRe(npts,npts)
real*8 zIm(npts,npts)
real*8 kRe(npts,npts)
real*8 kIm(npts,npts)
real*8 qRe(npts,npts)
real*8 qIm(npts,npts)
integer i,j,k,niter
! Number of iterations in the Mandelbrot
! fractal calculation
niter=51
do j=1,npts
do i=1,npts
! Generating z = 0 (real and
! imaginary part)
zRe(i,j)=0.
zIm(i,j)=0.
! Generating the constant k (real and
! imaginary part)
kRe(i,j)=dble(i)*2.0/(dble(npts)-1.)-1.5
kIm(i,j)=dble(j)*2.0/(dble(npts)-1.)-1.
enddo
enddo
! Iterating
! print *,"Calculating Mandel"
do k=1,niter
do j=1,npts
do i=1,npts
! Calculating q = z*z + k in complex space
! q is a temporary variable to store the result
qRe(i,j)=zRe(i,j)*zRe(i,j)-zIm(i,j)*zIm(i,j)+kRe(i,j);
qIm(i,j)=2.*zRe(i,j)*zIm(i,j)+kIm(i,j);
! Assigning the q values to z constraining between
! -5 and 5 to avoid numerical divergences
zRe(i,j)=qRe(i,j);
zIm(i,j)=qIm(i,j);
if (zRe(i,j) < -5.) zRe(i,j)=-5.;
if (zRe(i,j) > 5.) zRe(i,j)=5.;
if (zIm(i,j) < -5.) zIm(i,j)=-5.;
if (zIm(i,j) > 5.) zIm(i,j)=5.;
enddo
enddo
enddo
! Lines below this one are commented out when making
! the benchmark.
! Writing image to STDOUT
do i=1,npts
do j=1,npts
print *,log( sqrt(zRe(i,j)*zRe(i,j)+zIm(i,j)*zIm(i,j)) + 1.)
enddo
enddo
end program mandel
Qualitative comparison table
Table 1 below summarises the qualitative aspects mentioned in the previous sections.
Explanations for the table columns are:
- Language: the name of the language.
- Version: the version number of the language used in the benchmark test.
- Flags: compilation flags or command line switches used in the benchmark test.
- High-level: whether the language is a high-level, array-oriented, numerical calculation language or not.
- Syntax: the consistency of the syntax for the language statements and availability of array manipulation functions to avoid loops on array indices.
- Math and I/O functions: availability of mathematical functions and scientific file format reading functions.
- Price: free software or highly priced.
| Language | Version | Flags | High level | Syntax | Math and I/O functions | Price |
| C | gcc 3.3.5 20050117 (pre-release) | -O3 | No | Bad | Bad | Free |
| FORTRAN77 | gcc version 3.3.5 20050117 (pre-release) | -O3 | No | Bad | Bad | Free |
| PDL | 2.4.1 | None | Yes | Good | Fair | Free |
| IDL | 6.2 linux x86 m32 | None | Yes | Fair | Good | High |
| MATLAB | 7.1.0.183 (R14) Service Pack 3 | -nodisplay -nojvm | Yes | Fair | Good | High |
| Octave | 2.1.64 (i686-Suse-Linux) | None | Yes | Fair | Good | Free |
Table 1: Qualitative evaluation of the different languages.
Benchmarks
Benchmarks are a tricky business
Benchmarks are a tricky business. This is specially the case for matrix oriented languages like the ones shown here.
Explicit loops through matrix indices or if-statements should be avoided, since these statements can sometimes make the code much slower.
Most of the functions of these languages are very high-level ones, which perform several more or less complex tasks. Choosing some functions over others that globally provide the same numerical result can have a relatively high impact in the benchmark. A clear example is the implementation of the equivalent of the PDL clip function in MATLAB and Octave. Depending on the implementation adopted, one language was faster than the other. In this article, the solution that seems more natural to MATLAB programmers was adopted, but this technique, as seen in figure 3, gives some advantage to MATLAB. Whereas, the other solution (not shown here) gave Octave a slight advantage. Another example is the loop order in the C and FORTRAN languages. If the loop order of the matrix indices (i and j) is reversed a significant performance penalty is obtained.
In any case, this benchmark can serve the purpose of giving an order of magnitude of the execution speeds of each one of the languages, revealing whether they are comparable or not.
The system used was a PC with an Intel Pentium 4 processor running at 2.8GHz, with a cache size of 1024Kb and 512MB of RAM. The operating system was SuSE Linux 9.3 (i586) with kernel version 2.6.11.4-21.15-2mp.
In this benchmark, I have run the exact code that has been shown in the listings provided in this article, taking into account the following comments:
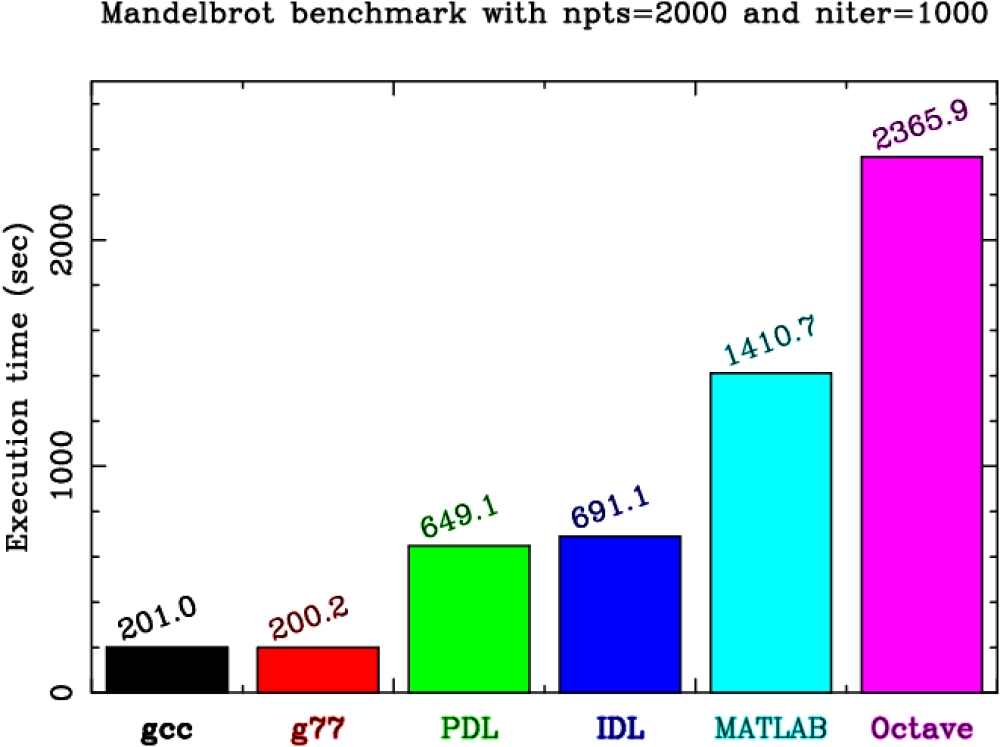
- Since these are number-crunching languages it seems reasonable to test them with big arrays. To obtain better accuracies in the benchmarks we have iterated the Mandelbrot algorithm many times. Thus, the benchmarks were done with
$npts=2000and$niter=1000. This effectively means that the benchmarks are done on 2000 x 2000 arrays and 1000 iterations. - The plotting routines were not included in the tests, only the number-crunching part. As highlighted in the comments in the code listings, the last lines of the code, which plot the graph, were commented out in the benchmarks.
- To measure the execution time the
timecommand was used. The final result shown in figure 3 is the sum of the system plus user time. To make the comparisons similar, in the case of C and FORTRAN, compilation times of the code has also been added to the final benchmark time. In any case, because of the long time spent in the 1000 iterations, this compilation or start-up time for any of the languages tested is really negligible compared with the total time. - The particular version of languages and compilation flags is shown in table 1.
Conclusion
High-level, matrix-oriented languages are a useful tool to develop projects with heavy numerical calculations or which require scientific plotting. With them it is relatively easy to obtain fast development cycles. This feature has been illustrated by generating the Mandelbrot fractal.
The qualitative comparison of several of these types of languages (PDL, IDL, MATLAB and Octave) can best be seen in table 1. Needless to say that such a comparison is very subjective.
The benchmarks on the examples (see figure 3) provided here show that some high-level, array-oriented languages like IDL or PDL, when properly coded to avoid array index loops and if statements, are only about three to four times slower than the faster, low-level languages like C or FORTRAN77. MATLAB and Octave perform similarly and they are clearly slower than IDL or PDL.
PDL wins hands down. It provides nearly the same or better capabilities than other more expensive proprietary solutions
From my personal point of view, PDL wins hands down. It provides nearly the same or better capabilities than other more expensive proprietary solutions. In particular, the mathematical and I/O functions provided by PDL are nearly equivalent to the ones from proprietary solutions and, in the case of array manipulation and language syntax, PDL is better. This comparison has no colour when price is considered, free vs. expensive. With PDL you will certainly never get a message like “No license available to run this software”, not to mention the risks of basing your programming projects on the decisions of the owners of the proprietary languages.